数据结构note（四）

发表于 更新于 分类于 ， Waline： 阅读次数： 本文字数： 4k 阅读时长 ≈ 4 分钟

栈和队列

栈和队列是限定插入和删除只能在表的“端点”进行的线性表。

  • 栈：其特点可以概括为“后进先出”。生活中比如手电筒的电池、手枪的弹匣等都可以视作“栈”，插入从尾部，删除也从尾部。（从一端插入和删除）

  • 队列：特点为“先进先出”，比如排队时最前面的人是最早来到这个队列也将最先离开队伍，插入从队尾插入，删除从队头删除。（从两端）

由于这两类结构分别所具有的这些特性在某些问题求解过程中也出现，故算法中也应利用“栈和队列”。

栈(stack)的定义和特点

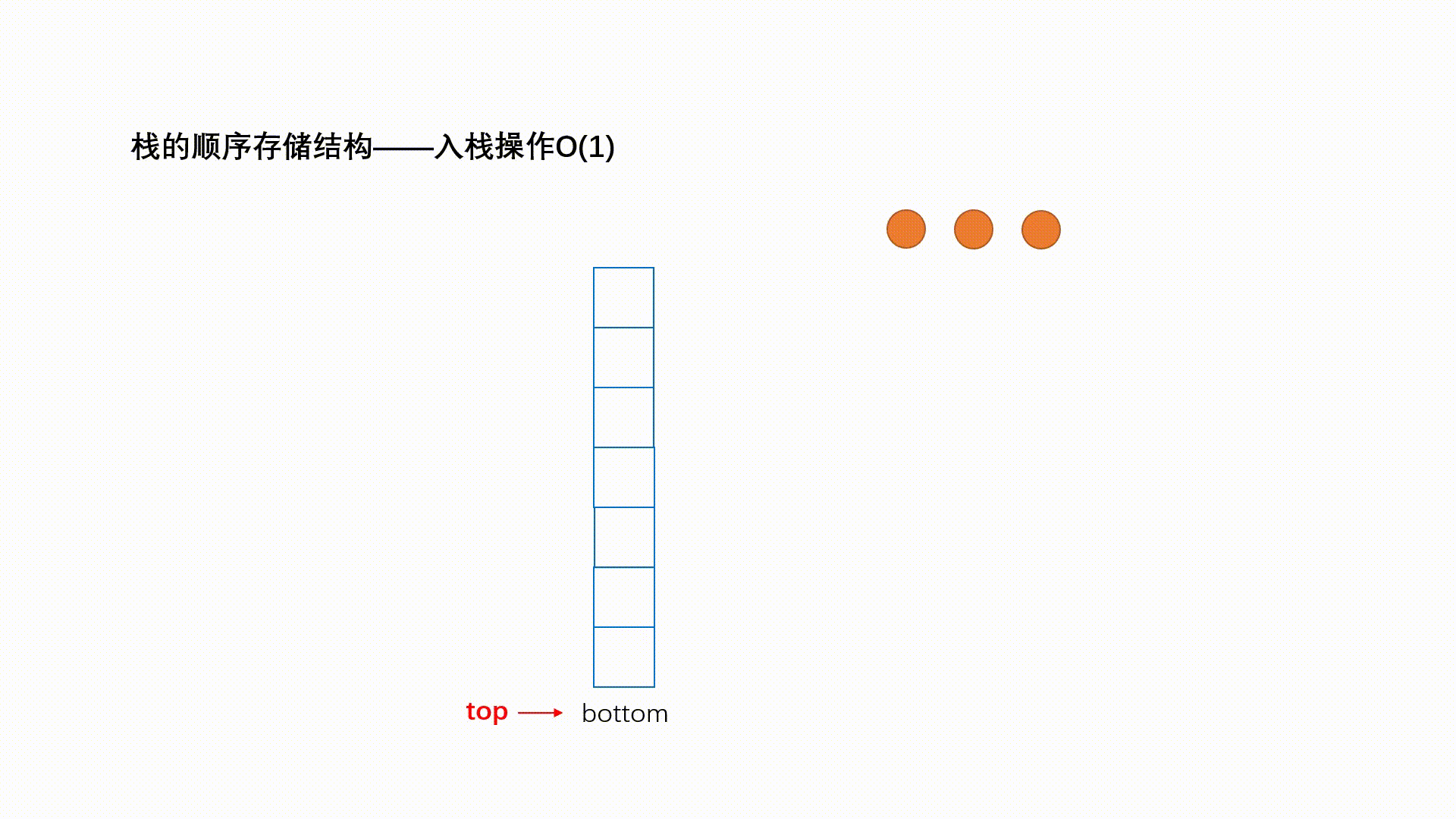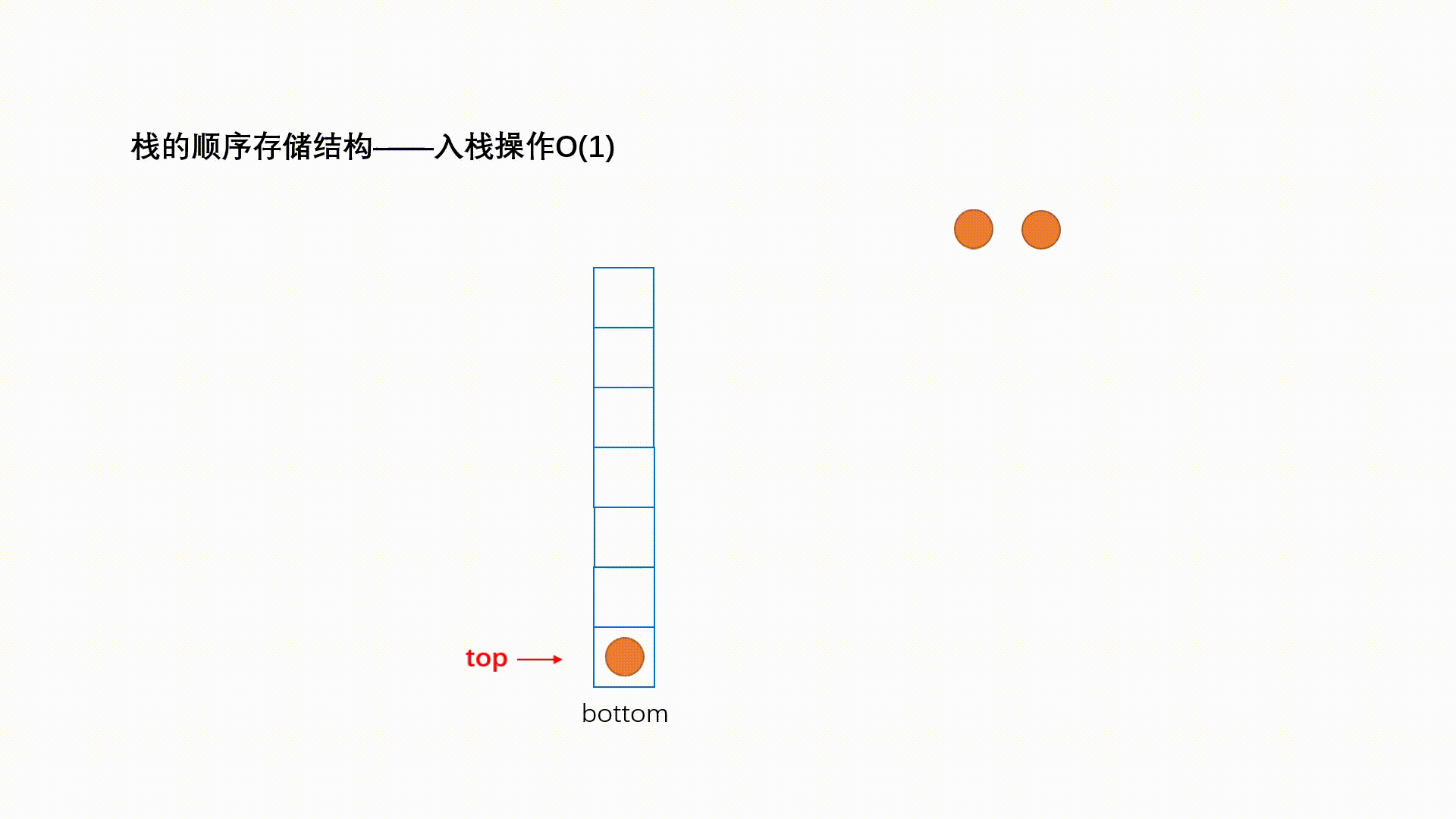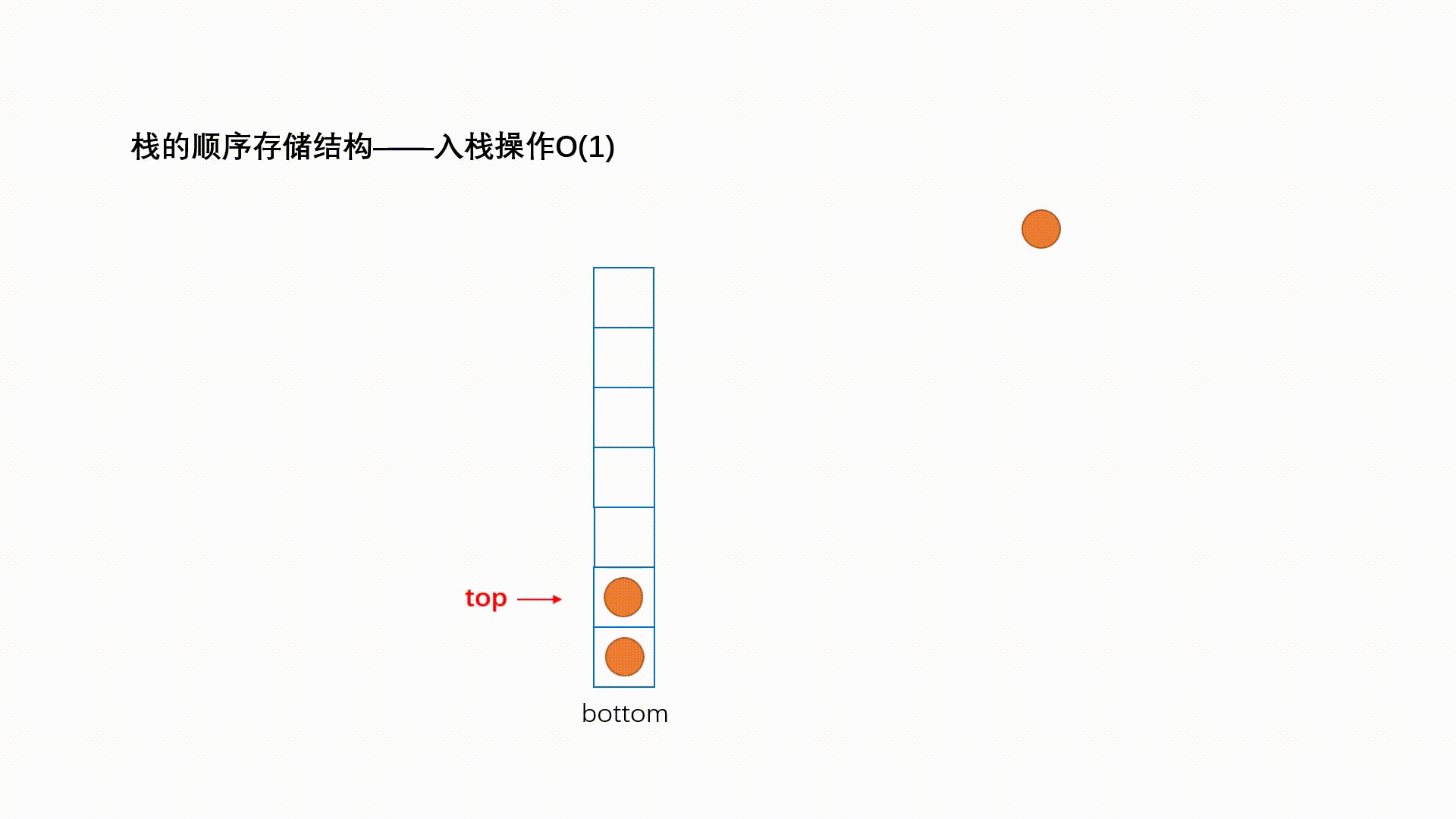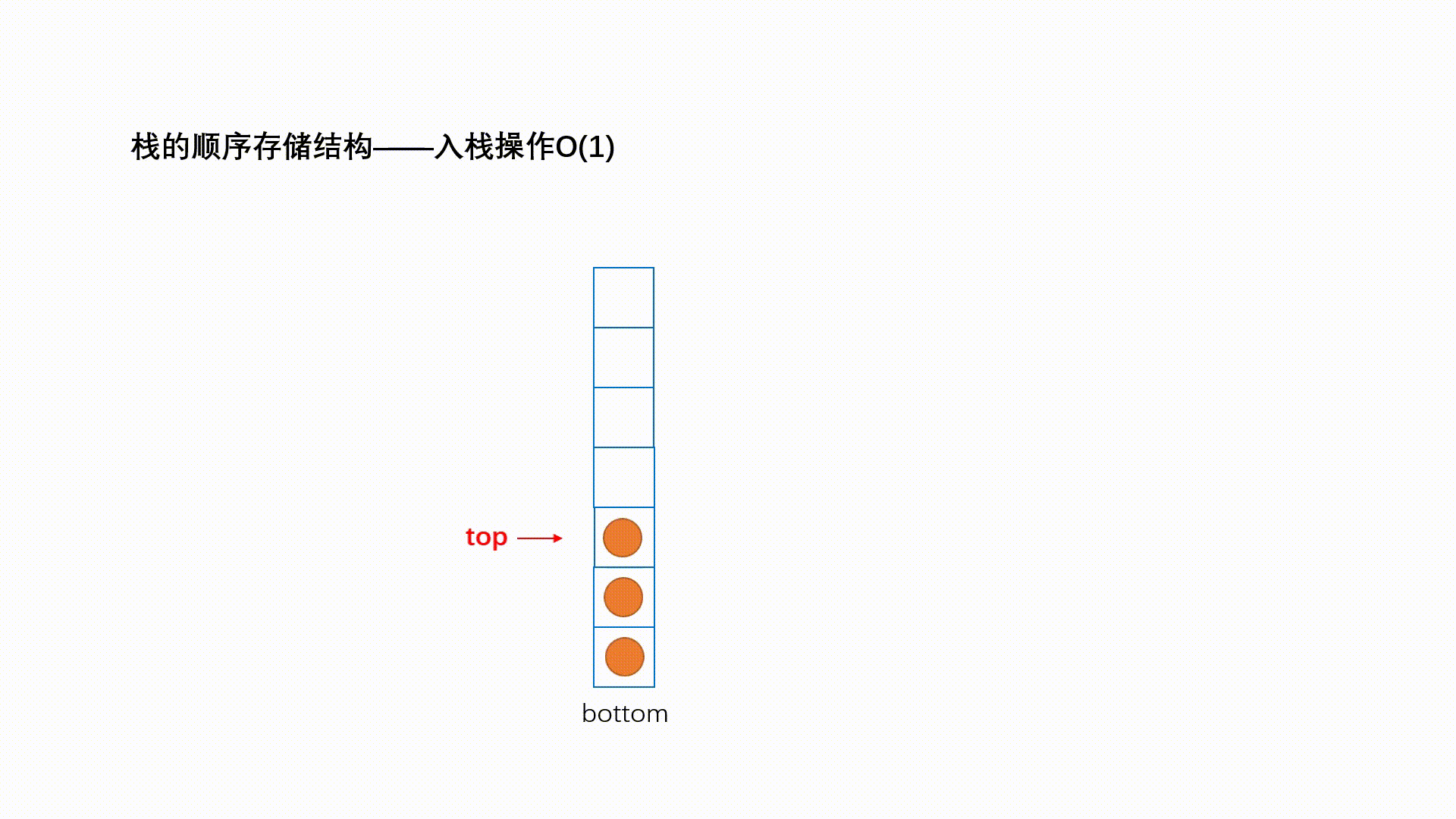
后进先出(Last In First Out)的线性表，简称LIFO结构，表尾an端称为栈顶（Top），表头a1端称为栈头（Base），通常用S表示栈。

队列(queue)的定义和特点

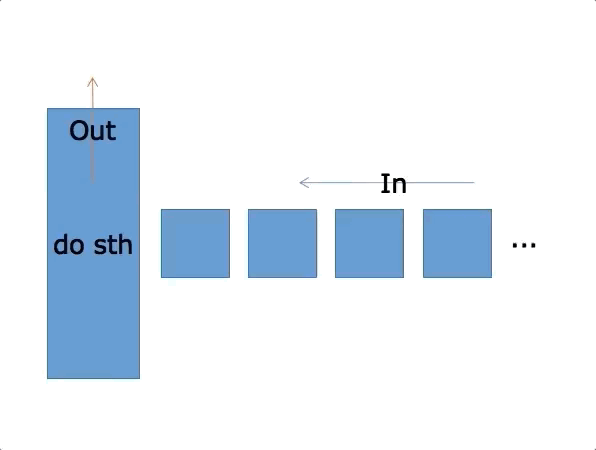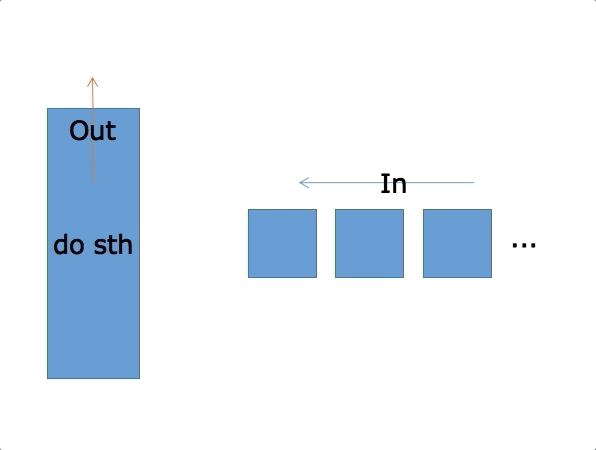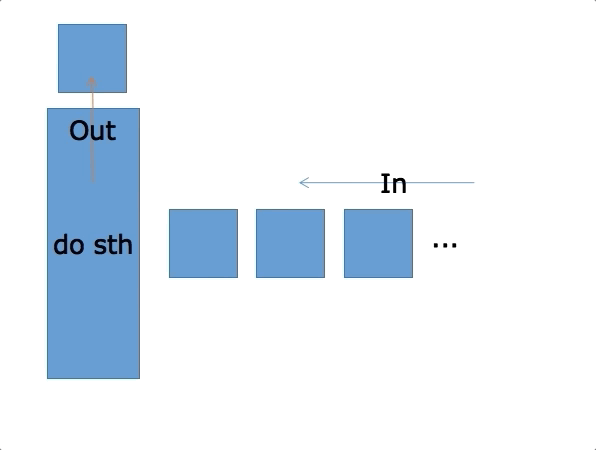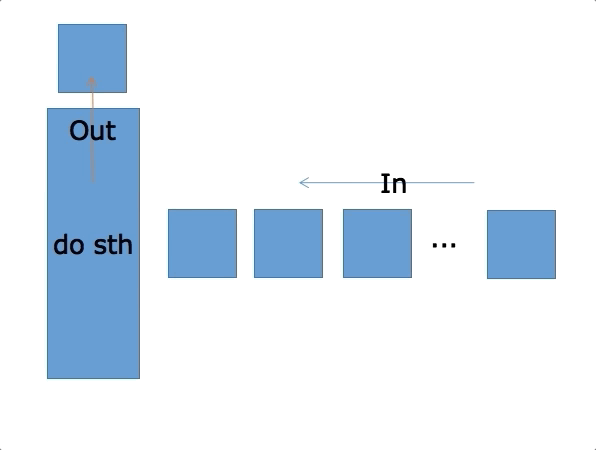
先进先出(First In First Out)的线性表，简称FIFO结构，在表的一端（表尾）插入，在另一端（表头）删除。通常用Q表示队列。

栈的实现（顺序栈）：

stack.h：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#pragma once
#define Maxsize 5//最大容量

class stack {
public:
    int stacksize; //表示栈可使用的最大容量
    int* top;//指向栈顶元素之上的位置
    int* base;
};

//初始化
stack Init_Stack();

//销毁栈
void Destroy_Stack(stack* s);

//判断栈是否空
bool ifEmpty_Stack(stack* s);

//求栈长度
int Length_Stack(stack* s);

//获取栈顶元素
int GetTop_Stack(stack* s);

//清空栈
void Clear_Stack(stack* s);

//入栈（插入元素）
void Push_Stack(stack* s, int e);

//出栈（弹出元素）
int Pop_Stack(stack* s);

stack.cpp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include "stack.h"
#include <iostream>

//初始化
stack Init_Stack() {
    stack s;
    s.stacksize = Maxsize;
    s.base = new int[Maxsize];
    s.top = s.base;
    return s;
}

//销毁栈
void Destroy_Stack(stack* s) {
    if (s->base != NULL) {
        delete s->base;
        s->stacksize = 0;
        s->base = s->top = NULL;
    }
}

//判断栈是否空
bool ifEmpty_Stack(stack* s) {
    if (s->top == s->base) {
        return true;
    }
    else{
        return false; 
    }
}

//求栈长度
int Length_Stack(stack* s) {
    return s->top-s->base;
}

//获取栈顶元素
int GetTop_Stack(stack* s) {
    return *(s->top-1);
}

//清空栈
void Clear_Stack(stack* s) {
    if(s->base != NULL){
        s->top = s->base;
    }//top指针指向栈底即可
}

//入栈（插入元素）
void Push_Stack(stack* s, int e) {
    if (s->top-s->base == s->stacksize) {
        return;
    }//判断是否满栈
    *s->top = e;
    s->top++;
    //上面的两步可以合并成一步：*s->top++ = e;
}

//出栈（弹出元素）
int Pop_Stack(stack* s) {
    if (s->top == s->base) {
        std::cout << "当前为空栈" << std::endl;
        return -1;
    }//判断是否空栈
    s->top--;
    return *s->top;
}

teststack.cpp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
#include "stack.h"
using namespace std;


int main()
{
    stack s = Init_Stack();
    cout << "栈状态为（1空0非空）：" << ifEmpty_Stack(&s) << endl;
    Push_Stack(&s, 1);
    cout << "栈状态为（1空0非空）：" << ifEmpty_Stack(&s) << endl;
    Push_Stack(&s, 2);
    Push_Stack(&s, 3);
    Push_Stack(&s, 5);
    Push_Stack(&s, 8);
    cout << "栈顶元素为：" << GetTop_Stack(&s) << endl;
    cout << "现在弹出：" << Pop_Stack(&s) << endl;
    cout<<"此时栈顶元素为：" << GetTop_Stack(&s) <<
        "   栈内元素有："<<Length_Stack(&s)<<"个" << endl;
    Clear_Stack(&s);
    cout << "清除后栈状态为（1空0非空）：" << ifEmpty_Stack(&s) << endl;
    Destroy_Stack(&s);

    system("pause");
    return 0;
}

队列的实现（循环顺序队列）：

由于只申请了MaxQSize大小的内存空间，且队头队尾指针均会在入队和出队的过程中后移，故当队尾溢出时有时并没有真正的超出给定的储存大小，这种现象被称为“假溢出”。解决假溢出的一种方法就是采用循环队列。

还有一个问题就是，判断队空或队满要比栈空或栈满麻烦一点，因为判断队空/满的条件是一样的，都是队空指针==队尾指针。解决的方法是加一个统计空间的变量或者少用一个存储空间。

下面仅陈列queue.cpp的定义部分。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include "queue.h"

//初始化队列
queue Init_Queue() {
	queue q;
	q.base = new int[MaxQSize];
	q.front = q.rear = 0;
	return q; 
}

//销毁队列
void Destroy_Queue(queue* q) {
	q->front = q->rear;
	delete q->base;
}

//清空队列
void Clear_Queue(queue* q) {
	q->front = q->rear = 0;
}

//获得队列长度
int Length_Queue(queue* q) {
	return (q->rear - q->front + MaxQSize) % MaxQSize;
}

//获取队头元素
int GetHead_Queue(queue* q) {
	if (q->front != q->rear) {
		return q->base[q->front];
	}
}

//入队
void EnQueue(queue* q,int data) {
	//判断队满
	if ((q->rear + 1) % MaxQSize == q->front) {
		return;
	}
	q->base[q->rear] = data;
	q->rear = (q->rear + 1) % MaxQSize;
}

//出队
int DeQueue(queue* q) {
	//判断队空
	if (q->front == q->rear) {
		return -1;
	}
	int e = q->base[q->front];
	q->front = (q->front + 1) % MaxQSize;
	return e;
}